Day 22 of Advent of Code 2021 was all about cubes. The problem statement provided us with coordinates of cubes and an “on” or “off” instructions. These instructions needed to be carried out in order. The first part of the problem was deceptively simple. So much so that I didn’t go for the “obvious” solution initially because I thought it wouldn’t scale. As it happened I ended up implementing it anyway as my optimised approach wasn’t working because I made a simple mistake.

Parsing the instructions

Before looking into solving the problem, the first step was to parse the instructions which were in the following format:

on x=10..12,y=10..12,z=10..12
on x=11..13,y=11..13,z=11..13
off x=9..11,y=9..11,z=9..11
on x=10..10,y=10..10,z=10..10

To start with, I set up my data types for these “instructions”:

1
2
3

type Vec = [Int]
type Cube = [Vec]
type Instruction = (Cube, Int)

What I determined (after some experimentation) was that the following notation was the nicest to work with:

• Vector for the top-left coordinate of the cube
• Vector for the bottom-right coordinate of the cube
• And 1 or -1 to determine whether the cube is to switched on (1) or off (-1)

The reason for this will become clearer in a minute, but for now, let’s define the parsers for turning the text into an instruction:

First, a parser combinator for a number:

1
2
3
4
5

p_num :: Parsec String () Int
p_num = do
  sign <- option ' ' (char '-')
  num <- many1 digit
  return (read $ sign : num)

This will read an optional sign, many numbers and return an integer.

Next, let’s define a range of numbers (1..6):

1
2
3
4
5
6

p_range :: Parsec String () Vec
p_range = do
  start <- p_num
  string ".."
  end <- p_num
  return [start, end+1]

For the range, I’ve added 1 to the end. I found having the end range defined [inclusive,exclusive) made it more intuitive. Again, a bit more on that later.

Then another parser combinator for the whole cube:

1
2
3
4
5
6
7
8
9

p_cube :: Parsec String () Cube
p_cube = do
  string "x="
  x <- p_range
  string ",y="
  y <- p_range
  string ",z="
  z <- p_range
  return $ sort $ transpose [x, y, z]

To point out here, when turning the X, Y, Z ranges into a cube, I used the transpose function such that we turn pairs [[10,13],[10,13],[10,13]] into 3D vectors to describe the cube. I think [[10,10,10],[13,13,13]] is easier to read.

1
2

*Common> parse p_cube "" "x=10..12,y=10..12,z=10..12"
Right [[10,10,10],[13,13,13]]

Finally, we just need to parse the whole instruction (the on and off bits):

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

p_on :: Parsec String () Int
p_on = do
  string "on"
  return 1

p_off :: Parsec String () Int
p_off = do
  string "off"
  return (-1)

p_instruction :: Parsec String () Instruction
p_instruction = do
  status <- try p_on <|> p_off
  string " "
  cube <- p_cube
  return (cube, status)

Part One

Now we’ve parsed the text, the first thought on how to tackle the problem was just to turn each cube into a set of coordinates [x,y,z] and then model the “on” and “off” instructions. First step was a function to convert a cube into a list of points within the cube:

1
2
3
4
5

dump :: Cube -> [Vec]
dump [[x1,y1,z1], [x2,y2,z2]] =
  [[x,y,z] | x <- [x1..x2-1],
             y <- [y1..y2-1],
             z <- [z1..z2-1]]

Haskell’s list comprehension and parameter destructuring comes in handy here!

Example:

1
2

*Common> dump [[1,1,1],[3,3,3]]
[[1,1,1],[1,1,2],[1,2,1],[1,2,2],[2,1,1],[2,1,2],[2,2,1],[2,2,2]]

Then it is a matter of using a Set to add and remove the cubes:

1
2
3
4
5

type CubeSet = Set Vec

mergeSet :: CubeSet -> Instruction -> CubeSet
mergeSet cs (c, 1) = cs `union` (fromList $ dump c)
mergeSet cs (c, -1) = cs `difference` (fromList $ dump c)

This will add/remove the points from the set and a fold can be used to process all the instructions

foldl mergeSet empty instructions

This folds over all the instructions, calling merge with each instruction.

As I mentioned previously, I hadn’t intended to implement it this way because I figured that there would be lots and lots of points - in the example alone there were 556,501 individual cuboids. I assumed that part one would have a few more cubes than that, such that the “count each individual cuboids” approach would not be feasible.

Turns out that for part 1 it was feasible. One important lesson here was for me not to assume that just because the approach was not going to scale, it wouldn’t actually work. I would have been able to complete part 1 a lot quicker if I had just tried the simplistic approach. In compute time it wasn’t as quick and wouldn’t scale, but as I didn’t actually know yet what part 2 was going to be, in hindsight I spent far too much effort there and should have remembered YAGNI…

Part Two

As it turns out, my effort of optimising the calculation was not in vain as when I opened the description of the second part it was immediately obvious that the simplistic approach wasn’t going to work. The example solution was to count 2,758,514,936,282,235 individual cuboids. That’s 2,800 trillion. If I was going to model them as individual cuboids, I was going to run out of memory very quickly!

First Attempt

Clearly I had to change my thinking around splitting up each instruction into individual cuboids, to something that deals with cubes, we’ve got two scenarios:

Firstly, when adding cubes, what we’re doing is (explaining in two dimensions, principle is the same in three dimensions)

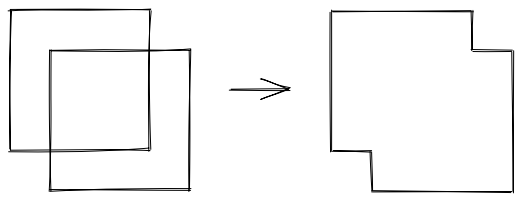
And when removing cubes:

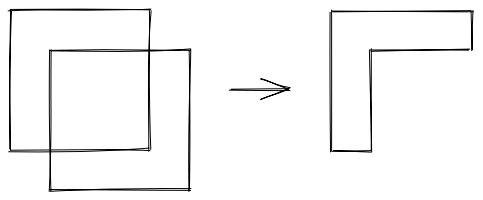
The problem with calculating the overall volume of the cubes is that if we just add up all the volumes, we’re double counting individual cuboids if they’re contained in multiple cubes.

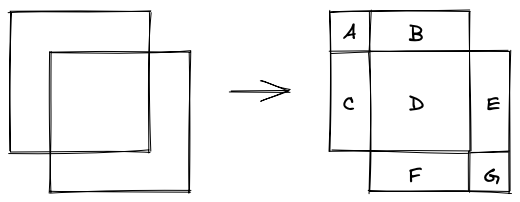
So if I split up my original cubes into lots of smaller cubes, then I can remove the duplicate ones (i.e. the ones covered by both cubes). So for the addition, I would pick cube A, B, C, D, E, F, G. If the second cube is removed, then I would only pick A, B, C. The for the next step I can just work with these smaller cubes.

Back to some code, I can just calculate the volume of each cube:

1
2
3

volume :: Cube -> Int
volume [a, b] = 
  product $ zipWith (\a' b' -> max 0 $ b' - a') a b

To unpack this:

• The zipWith function allows me to join two lists together. As both my top-left and bottom-right vectors are lists with 3 elements (x, y, z), this means I just want to subtract the greater from the smaller.
• Then max 0 ensures that any negative values are set to 0. This ensures that the volume of an invalid cube (where the top-left is greater than the bottom-right) returns a volume of 0. Note, initially I had a bug in this function which meant that if the top-left was greater on two axis, because two negatives make a positive, I would get back positive volumes for a cube that shouldn’t be counted. Took me a long time to figure this out.
• At the end I multiply the 3 subtractions together using product, giving me the volume of the cube.

Next, I define the intersection of two cubes:

1
2
3

inter :: Cube -> Cube -> Cube
inter [a1, a2] [b1, b2] = 
  [zipWith max a1 b1, zipWith min a2 b2]

Again, the destructuring of parameters and the zipWith function makes this quite straightforward. To get the intersection between two cubes, I just combine their top-left and their bottom-right vectors. For example:

1
2

*Common> [[1,1,1],[4,4,4]] `inter` [[2,2,2],[6,6,6]]
[[2,2,2],[4,4,4]]

Note, by putting a function in backticks, it can be turned into an operator, the above is the equivalent of

1
2

*Common> inter [[1,1,1],[4,4,4]] [[2,2,2],[6,6,6]]
[[2,2,2],[4,4,4]]

Next, using intersection and volume, I could create a function that allowed me to check whether two cubes were actually intersecting:

1
2

overlaps :: Instruction -> Instruction -> Bool
overlaps (c, _) (c', _) = (>0) $ volume $ inter c c'

This just pulls out the cubes from each of the “instructions”, calculates the volume of the intersection. If the volume is greater than 0, then the two overlap.

Now it was just a matter of splitting up overlapping cubes into lots of little cubes. And after some encouraging results, I found that splitting each cube into lots of little cubes just exponentially create more cubes and I still sat there looking at my terminal window for over a minute and then thinking, nah and hitting Ctrl-C.

Second Attempt

So I went back to the drawing board and thought that I needed to simplify, so I took another look at my 2D drawing:

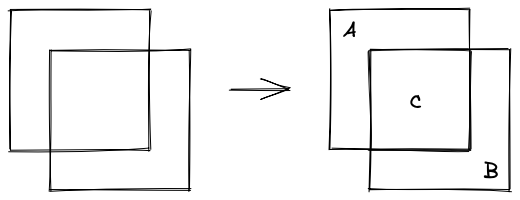
Now, the problem was that when I am looking at my three cubes (again, for simplicity drawn in 2D shapes), when I was looking at it in the REPL:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

*Common> a = [[1,1,1],[5,5,5]]
*Common> b = [[3,3,3],[7,7,7]]
*Common> c = a `inter` b
*Common> c
[[3,3,3],[5,5,5]]
*Common> volume a
64
*Common> volume b
64
*Common> volume c
8

I had cubes A and B each with a volume of 64 (4 cubed) and if I intersect A and B, I get another cube C, which has a volume of 8 (2 cubed). Now if I wanted to calculate the total number of cuboids covered, I can just do:

1
2

*Common> volume a + volume b - volume c
120

Looking at it another way, the area that is covered by both cubes A and B (the intersecting cube C) is double counted, so if we add an intersecting cube that counts each cuboid negatively, we get the correct count. That way, we can work out the count without splitting every cube into lots of tiny cubes.

To do this in code:

1
2
3
4
5

merge :: Instruction -> Instruction -> Instruction
merge (a, 1) (b, 1) = (inter a b, -1)
merge (a, -1) (b, -1) = (inter a b, 1)
merge (a, 1) (b, -1) = (inter a b, -1)
merge (a, -1) (b, 1) = (inter a b, 1)

The above creates the “adjusting cube” that would remove any double-counted cuboids. We’ve already gone through the scenario of adding two cubes (A + B) in the above image. What about removing? Then we just need to add an adjustment of -1 for the intersecting cube. Similarly, if we have a negative cube and are adding a positive cube, then adding an adjusting cube of an extra 1 will ensure the count is correct.

So when we merge two “instructions” - i.e. cube with on (+1) or off (-1) - we just do the following:

1
2
3
4
5
6

mergeAll :: [Instruction] -> Instruction -> [Instruction]
mergeAll is i = dedupe $ (mergeAll' is i) ++ (map (`merge` i) $ findOverlaps is i)

mergeAll' :: [Instruction] -> Instruction -> [Instruction]
mergeAll' is i@(_, 1) = i : is
mergeAll' is (_, -1) = is

Unpacking this a bit:

• The mergeAll function takes the existing list (is) and finds the overlaps of the new cube, and then uses merge to add the adjusting cubes.
• If it’s an “add”, then we add the cube
• If it’s a “remove”, then we don’t add the cube (as it’s just an instruction to remove)

This can then be used like so:

1

sum $ map cuboids $ foldl mergeAll [] instructions

• The foldl uses mergeAll to process all the instruction
• map cuboids calculates the adjusting volume of each cube (adding or subtracting)
• sum adds it all up

And with that the calculations complete in about 6 seconds (there’s probably still lots of optimising to do but it was good enough for the puzzle!)

Rest of the solution on GitHub

Conclusion

I found this puzzle quite instructive. The lesson was not to overcomplicate things! I tried to be clever and solve it generally to start with when it turned out I could have done the less optimal solution for part one and still finish in a reasonable time. Like in previous challenges I also found that a good solution feels elegant. There were times when I was working on my first approach that I felt I was onto a winner with my cube splitting approach and was quite shocked when even the example to too long to compute. My solution got more and more convoluted and eventually I decided to start again from scratch. I’m really pleased with that as I think the solution I ended up with is quite elegant.

One last note, the main thing that held me up was the subtle bug I had in the volume function. If I had added a few more edge test cases early, I would have saved myself quite a lot of debugging. Chalk one up for good testing makes things quicker!

If you'd like to find more of my writing, why not follow me on Bluesky or Mastodon?